
Drawing of Geometrical figures angles, Triangle, Circle, Rectangle, Square, Parallelogram and single stroke lettering and numbering drawing is here.
Angles and Triangles
Measurement and types of angles, and types of angle and triangle is given below.Angles: Angle is the inclination between two straight lines meeting at a point or meet when extended. AB and BC are two straight lines meeting at B. The inclination between them is called an angle. The angle is expressed in degrees or radians.
Triangle: Triangle is a closed plane figure having three sides and three angles. The sum of the three angles always equals to 180°.
Types of angles
Acute angle: If an angle which is less than 90° is called an acute angle.
Right angle: Angle between a reference line and a perpendicular line is called right angle.
Obtuse angle: This refer to an angle between 90° and 180°.
Straight angle: This refers to an angle of 180°. This is also called as the angle of a straight line.
Reflex angle: It is the angle which is more than 180°.
Adjacent angles: These are the angles lying on either side of a line.
Complementary angles: When the sum of the two angles is equal to 90°, angle POQ + angle QOR = 90° angle POQ and angle QOR are complementary angles to each other.
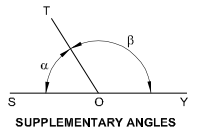
Supplementary angle: When the sum of the two adjacent angles is equal to 180°, example angle SOT + angle TOY = 180o, angle SOT and angle TOY are supplementary angles to each other.
Types of triangles
Equilateral triangle: is a triangle having all the three sides equal. Also all the three angles are equal (60°).
Isosceles triangle: has two of its sides equal. The angles opposite to the two equal sides are also equal.
Scalene triangle has all the three sides unequal in lengths. All the three angles are also unequal.
Right angled triangle: is one in which one of the angles is equal to 90° (Right angle). The side opposite to right angle is called hypotenuse.
Acute angled triangle: is one in which all the three angles are less than 90°.
Obtuse angled triangle: has one of the angles more than 90°.
Geometrical figures
Square: In a square all the four sides are equal and its four angles are at right angles. The two diagonals are equal and perpendicular to each other.
Rectangle: In a rectangle, opposite sides are equal and parallel and all four angles are right angles.

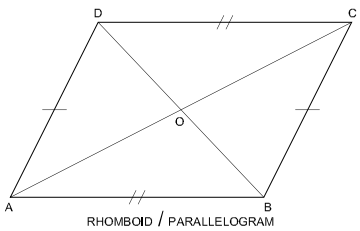
Parallelogram: In a parallelogram opposite sides are equal and parallel. Opposite angles are also equal. Diagonals are not equal but bisect each other.
Circle: Circle is a plane figure bounded by a curve, formed by the locus of a point which moves so that it is always at a fixed distance from a stationery point the "Centre".
Circle: Circle is a plane figure bounded by a curve, formed by the locus of a point which moves so that it is always at a fixed distance from a stationery point the "Centre".
Radius: The distance from the centre to any point on the circle is called the "Radius".
Diameter: The length of a straight line between two points on the curve, passing through the centre is called the "Diameter". (D: Dia or d) It is twice the radius.
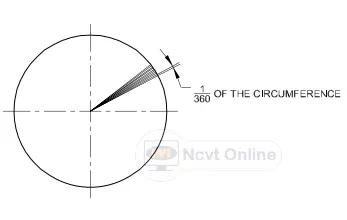
Circumference: It is the linear length of the entire curve, equal to D .
Arc: A part of the circle between any two points on the circumference or periphery is called an 'Arc'.
Chord: A straight line joining the ends of an arc is called the chord. (Longest chord of the circle is the diameter)
Segment: A part of the circle or area bound by the arc and chord is the segment of the circle.
Sector: It is the part of a circle bounded by two radii (plural of radius) meeting at an angle and an arc.
Quadrant: Part of a circle with radii making 90o with each other is a quadrant (one fourth of the circle).
Half of the circle is called as semi-circle.
Half of the circle is called as semi-circle.
Tangent: Tangent of a circle is a straight line just touching the circle at a point. It does not cut or pass through the circle when extended. The point where the tangent touches the circle is called the "point of tangency". The angle between the line joining the centre to the point of
tangency and the tangent is always 90°.
Concentric circles: When two or more circles (drawn) having common centre, they are called concentric circles. Ball bearing is the best example of concentric circles.
tangency and the tangent is always 90°.
Concentric circles: When two or more circles (drawn) having common centre, they are called concentric circles. Ball bearing is the best example of concentric circles.
Lettering and numbering - Single stroke
Apart from graphical elements (lines, arcs, circles etc) technical drawings will also contain written information. These written information are referred as “lettering”.Styles of lettering: Many styles of lettering are in use to day. However, a few styles which are commonly used are shown in below.
Standard heights/Width: The standard heights recommended by BIS SP: 46-2003 are in the progressive ratio of “square root 2”. They are namely 2.5 - 3.5 - 5 - 7 - 10 - 14 and 20 mm. The height of lower case letter (without tail or stem) are 2.5, 3.5, 5, 7, 10 and 14 mm. There are two standard ratios for the line thickness “d”. They are A & B. In A = line thickness (d) is h/14 and in B=line thickness (d) is h/10.
Lowercase means small letters, as
uppercase to capital letters. The width of different letters in terms of “d” is as follows
ED 1st Year Other Topics for Electrical Trades
Electrical Trades - Electrician, Wireman, Electroplater, Lift & Escalator Mechanic, Electrician Power Distribution. Select Engineering Drawing 1st Year topic from below.
